In this article, we will learn about binary search trees. We will study the underlying concepts behind binary search trees and then implement the code. You should be familiar with the concepts of binary trees to read this article.
What is a binary search tree?
A binary search tree is a binary tree data structure with additional properties along with the properties of binary trees. In a binary search tree,
- There are no duplicate values.
- The left subtree of a node has all the data values less than its own data. i.e. The left child or children of the left child are always less than the value in the current node.
- The right subtree of a node has all the data values greater than its own data. i.e. The right child or children of the right child of the current node are always greater than the current node.
This can be observed in the following Example.
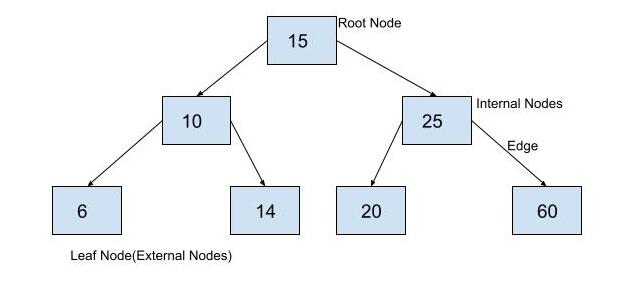
Implementation of Binary Search Tree in Python
To implement a Binary Search Tree, we will use the same node structure as that of a binary tree which is as follows.
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild=None
Now, to implement a binary search tree, we will implement functions to insert a value in the tree, search a value in the binary tree, and then we will see how to find the minimum and maximum elements from the binary search tree.
Insertion of a node in Binary Search Tree
While inserting a node in a binary search tree, three conditions may arise.
- The Binary search tree can be empty. i.e. Root itself will be a value None.
- The Value to be inserted is less than the root.
- The value to be inserted is greater than the root.
To implement the first condition, we just make a new node and declare it as root. To implement second and third condition, We follow the following approach.
From the properties of a binary search tree, we can see that each sub tree is a binary search tree in itself. Thus we can consider each node as a root of another binary tree.
While inserting a new node, if the value of the new data is less than the value of the current node, we will add it to the left child of the binary search tree, otherwise, we will add it to the right child.
Proceeding recursively, we will always reach the first condition and then we will declare a new node and add the node to the binary search tree.
Following is the implementation of above approach.
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild=None
def insert(root,newValue):
#if binary search tree is empty, make a new node and declare it as root
if root is None:
root=BinaryTreeNode(newValue)
return root
#binary search tree is not empty, so we will insert it into the tree
#if newValue is less than value of data in root, add it to left subtree and proceed recursively
if newValue<root.data:
root.leftChild=insert(root.leftChild,newValue)
else:
#if newValue is greater than value of data in root, add it to right subtree and proceed recursively
root.rightChild=insert(root.rightChild,newValue)
return root
root= insert(None,15)
insert(root,10)
insert(root,25)
insert(root,6)
insert(root,14)
insert(root,20)
insert(root,60)
a1=root
a2=a1.leftChild
a3=a1.rightChild
a4=a2.leftChild
a5=a2.rightChild
a6=a3.leftChild
a7=a3.rightChild
print("Root Node is:")
print(a1.data)
print("left child of node is:")
print(a1.leftChild.data)
print("right child of node is:")
print(a1.rightChild.data)
print("Node is:")
print(a2.data)
print("left child of node is:")
print(a2.leftChild.data)
print("right child of node is:")
print(a2.rightChild.data)
print("Node is:")
print(a3.data)
print("left child of node is:")
print(a3.leftChild.data)
print("right child of node is:")
print(a3.rightChild.data)
print("Node is:")
print(a4.data)
print("left child of node is:")
print(a4.leftChild)
print("right child of node is:")
print(a4.rightChild)
print("Node is:")
print(a5.data)
print("left child of node is:")
print(a5.leftChild)
print("right child of node is:")
print(a5.rightChild)
print("Node is:")
print(a6.data)
print("left child of node is:")
print(a6.leftChild)
print("right child of node is:")
print(a6.rightChild)
print("Node is:")
print(a7.data)
print("left child of node is:")
print(a7.leftChild)
print("right child of node is:")
print(a7.rightChild)
Output:
Root Node is:
15
left child of node is:
10
right child of node is:
25
Node is:
10
left child of node is:
6
right child of node is:
14
Node is:
25
left child of node is:
20
right child of node is:
60
Node is:
6
left child of node is:
None
right child of node is:
None
Node is:
14
left child of node is:
None
right child of node is:
None
Node is:
20
left child of node is:
None
right child of node is:
None
Node is:
60
left child of node is:
None
right child of node is:
None
In the above output, we can verify every property of the binary search tree in our example. Here, after declaring the root node, no matter what the order of insertion of elements is there, the output will always be the same. Try this by copying and pasting this code in your own python IDE.
Searching an element in a binary search tree
We have seen above that a node with a value less than that of the current node’s value will always be in the left subtree of the current node and a node with a value greater than that of the current node’s value will always be in the right subtree of the current node. We will use this property to search an element in a binary search tree.
- If the current node becomes empty, i.e. None, the element to be searched isn’t present in the tree and we will return False.
- If the current node has a value equal to the search query, we will return True.
- If the value to be searched is greater than the current node’s value, we will search the right subtree of the current node.
- If the value to be searched is less than the current node’s value, we will search the left subtree of the current node
Implementation of the logic is given below.
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild=None
def insert(root,newValue):
#if binary search tree is empty, make a new node and declare it as root
if root is None:
root=BinaryTreeNode(newValue)
return root
#binary search tree is not empty, so we will insert it into the tree
#if newValue is less than value of data in root, add it to left subtree and proceed recursively
if newValue<root.data:
root.leftChild=insert(root.leftChild,newValue)
else:
#if newValue is greater than value of data in root, add it to right subtree and proceed recursively
root.rightChild=insert(root.rightChild,newValue)
return root
def search(root,value):
#Condition 1
if root==None:
return False
#Condition 2
elif root.data==value:
return True
#Condition 3
elif root.data <value:
return search(root.rightChild,value)
# Condition 4
else:
return search(root.leftChild,value)
root= insert(None,15)
insert(root,10)
insert(root,25)
insert(root,6)
insert(root,14)
insert(root,20)
insert(root,60)
print(search(root,14))
print(search(root,22))
Output:
True
False
How to find the maximum element of a Binary Search Tree?
From whatever we have seen so far, we know that an element greater than the current node is always on its right side.
When we move to the right child of each node starting from root till end recursively, the greatest element will be present at the end.
So, to find the largest element of a binary search tree, we just have to find the rightmost element of the tree. Here is the implementation of this logic.
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild=None
def insert(root,newValue):
#if binary search tree is empty, make a new node and declare it as root
if root is None:
root=BinaryTreeNode(newValue)
return root
#binary search tree is not empty, so we will insert it into the tree
#if newValue is less than value of data in root, add it to left subtree and proceed recursively
if newValue<root.data:
root.leftChild=insert(root.leftChild,newValue)
else:
#if newValue is greater than value of data in root, add it to right subtree and proceed recursively
root.rightChild=insert(root.rightChild,newValue)
return root
def findLargestElement(root):
#check if binary search tree is empty
if root==None:
return False
#check if current node is rightmost node
elif root.rightChild==None:
return root.data
#check right subtree of current node
else:
return findLargestElement(root.rightChild)
root= insert(None,15)
insert(root,10)
insert(root,25)
insert(root,6)
insert(root,14)
insert(root,20)
insert(root,60)
print("Largest Element is:")
print(findLargestElement(root))
Output:
Largest Element is:
60
How to find smallest element of a binary search tree?
We know that an element lesser than the current node is always on its left side. When we move to the left child of each node starting from root till end recursively, the smallest element will be present in the last.
So, to find the smallest element of a binary search tree, we just have to find the leftmost element of the tree. Here is the implementation of this logic.
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild=None
def insert(root,newValue):
#if binary search tree is empty, make a new node and declare it as root
if root is None:
root=BinaryTreeNode(newValue)
return root
#binary search tree is not empty, so we will insert it into the tree
#if newValue is less than value of data in root, add it to left subtree and proceed recursively
if newValue<root.data:
root.leftChild=insert(root.leftChild,newValue)
else:
#if newValue is greater than value of data in root, add it to right subtree and proceed recursively
root.rightChild=insert(root.rightChild,newValue)
return root
def findSmallestElement(root):
#check if binary search tree is empty
if root==None:
return False
#check if current node is leftmost node
elif root.leftChild==None:
return root.data
#check right subtree of current node
else:
return findSmallestElement(root.leftChild)
root= insert(None,15)
insert(root,10)
insert(root,25)
insert(root,6)
insert(root,14)
insert(root,20)
insert(root,60)
print("Smallest Element is:")
print(findSmallestElement(root))
Output:
Smallest Element is:
6
Conclusion
In this article, we have seen underlying concepts behind binary search trees. We have also implemented various operations like insertion, searching, finding the maximum element, and finding a minimum element in the binary search tree.
I would encourage you to implement the codes and play with them. Stay tuned for more informative tutorials.
Happy Learning.



