Converting Base10 integer into a Base64 representation in Python will be learned in the article. Let us go through each and every pointer and concept so that we can gain thorough knowledge about this concept.
Number System and Need for Different Representation
Computations and measurements are enabled by the fundamental units of mathematics, which are numbers. The positional notation of the well-known decimal Base-10 system makes understanding it simple. Alternative bases, such as binary, octal, and hexadecimal, are needed in the digital world, though, for benefits like electronic logic correspondence and compact storage.
A balance is struck with the 64-character layout between machine efficiency and human readability. This pursuit of diverse numerical representations is not new; historically, different cultural expressions were reflected in different numeral systems. Investigating Base10 to Base64 conversion in Python reveals how common math and digital innovation are combined, linking human communication and computer processing.
Significance of Converting Base10 to Base64
In many different fields, utmost importance is given to the conversion of Base10 to Base64. Due to its compactness, data transmission is assured to be effective in the current fast-paced communication environment. It is important for images in online content or sending encrypted messages with security that the text can be readable by humans, which is possible with the conversion of binary data.
By converting the data, cross-platform interoperability is ensured, and standardized data interpretation is made possible. Base64 optimizes memory utilization while offering an understandable debugging format in environments with constrained resources. Insertion of content is accelerated by multimedia embedding through this function.
Base10 to Base64 conversion broadens possibilities by fusing mathematics and digital data manipulation, improving transmission, security, and usability in a complex technological environment.
Understanding the Number System
Base10
Base 10 is often known as the decimal system, which is the foundation of mathematics and the basis for how humans understand numbers. Base10, which has ten symbols (0–9), conveys quantities with ease by giving the positions of each digit weight through powers of 10.
Understanding amounts is simplified for us, and our daily computations are shaped by this system’s intuitive positional notation. Measurements, financial transactions, and a huge number of other aspects of daily life all benefit from Base10. Base10 plays a crucial part in our numerical knowledge, demonstrating its ongoing relevance as it serves as a link between human knowledge and mechanical processes in the digital world.
Base64
A flexible encoding technique called Base64 transforms binary data into sharable ASCII characters. Interoperability across platforms with 64 characters is guaranteed. The elegance of Base64 rests in its capacity to encrypt data for seamless web embedding, including audio, video, and graphics. It’s the digital connection between data and understanding, not just the encoding.
Common Use Cases
Base64 encoding, a pillar of contemporary data processing, has a wide range of uses. In situations where effective data transport is required, it performs well. For email attachments, URLs, and web requests, their concise representation is advantageous. Base64 is an essential component of secure key exchange in cryptography.
Additionally, seamless multimedia integration into web content eases file management challenges
How it Converts Binary Data into ASCII Characters
Base64’s binary-to-text conversion is what gives it its magic. It divides binary data into 24-bit values for each of the chunks. Mapping these values to a subset of 64 ASCII letters simplifies complex data. Base64 bridges the binary-text divide by padding missing portions with ASCII characters to create a mosaic of ASCII characters.
Conversion Process
Step-by-Step Process of Converting Base10 to Base64
We employ a methodical process to change a Base-10 number to Base64. Take the Base-10 integer 1839 as an example. We divide it by 64 several times, observing the results at each iteration. 28 is the quotient after the first division, leaving 71 as the remaining number.
The remaining data is represented by the Base64 character ‘G’. We achieve a new quotient of 0 and a remainder of 28, which represents the letter “A,” by carrying on with the quotient. The Base64 representation of “AG” is obtained by reversing the order of the remainders.
Divide and Remainder Method
Take the Base10 integer 12345 as our starting point as we explore the divide-and-remainder method. We get a quotient of 192 and a remainder of 33 when we divide 12345 by 64. The remaining value, 33, corresponds to the Base64 character ‘h’.
With the new quotient, 192, we proceed with this operation. It produces a quotient of 3 and a remainder of 0 when it is divided by 64 once more. The character ‘A’ is represented by the remaining 0 value. As a result, “hA” is used to represent 12345 in Base64.
Python Implementation
Using Built-in Functions
Base64 Module
Base64 encoding and decoding are made simple by the base64 module in Python. In order to transmit data, perform cryptographic procedures, and smoothly include multimedia content into a variety of applications, it provides functions to transform binary data into ASCII characters and vice versa.
To learn more about the Base64 Module, please read through the article.
Let’s see an example of how Base64 module is used to convert Base10 representation to Base64 representation
import base64
base10_number = 1839
base64_representation = base64.b64encode(str(base10_number).encode()).decode()
print(f"Base10 integer: {base10_number}")
print(f"Base64 representation: {base64_representation}")
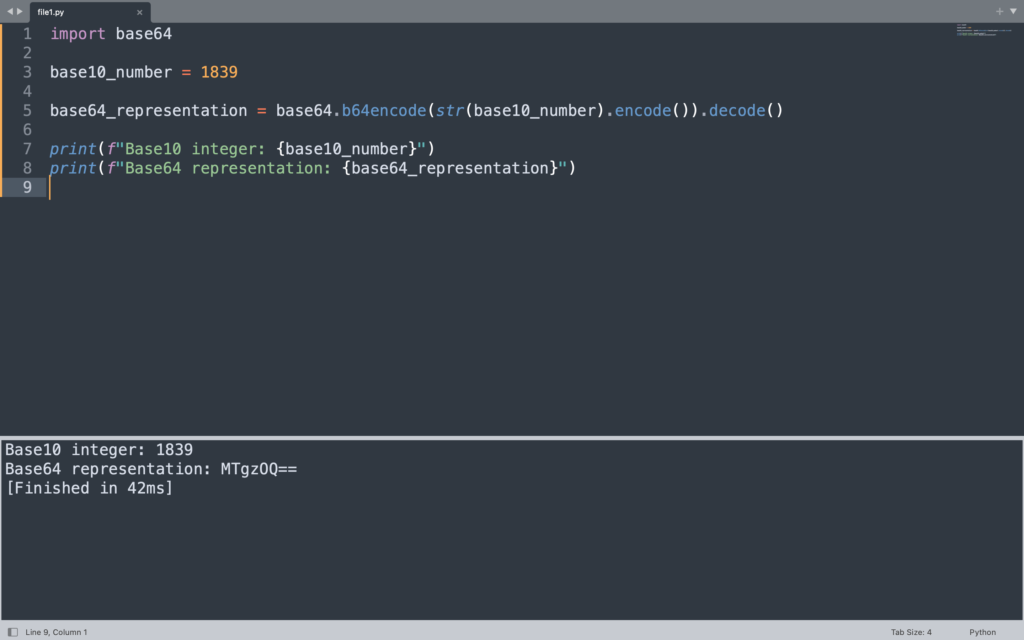
Using the base64.b64encode() function, the Base10 number is converted to a string, encoded as bytes, and then converted once again. Both the original Base10 integer and its equivalent Base64 representation are shown in the output, which illustrates the conversion process.
Manual Conversion
In the previous section, we learned how to do the conversion using the built-in function, but in some cases, you might want to implement the same functionality yourself. For this purpose, we will need some basic knowledge of math, and then we can follow along with the example given below:
number = 12345
base10_number = number
base64_chars = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
base64_representation = ""
while base10_number > 0:
remainder = base10_number % 64
base64_representation = base64_chars[remainder] + base64_representation
base10_number //= 64
print(f"Base10 integer: {number}")
print(f"Manual Base64 representation: {base64_representation}")
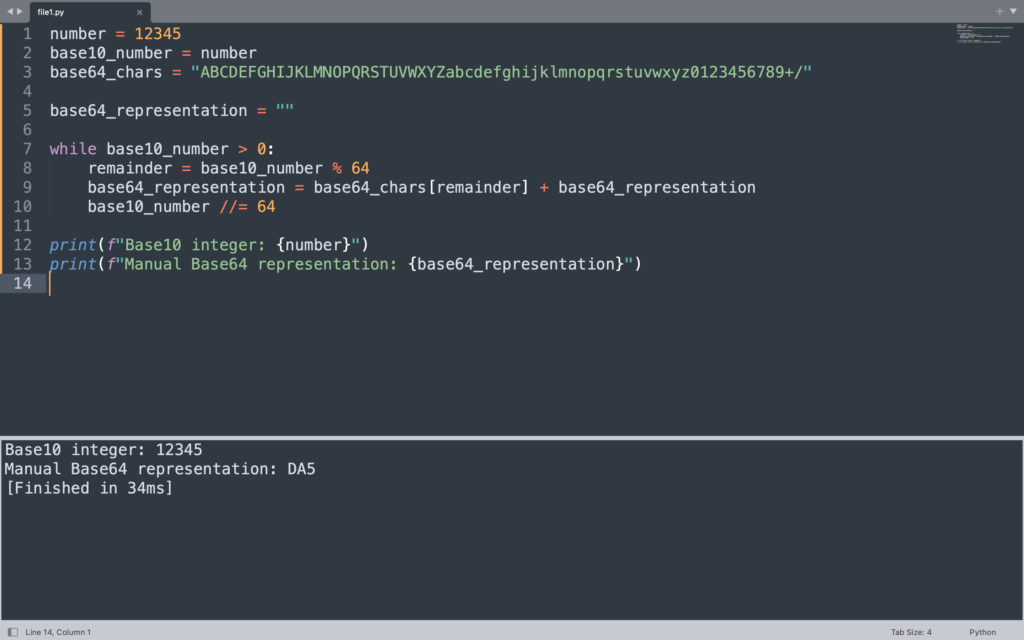
We define the Base10 integer and Base64 character sets in this code. The Base10 number is repeatedly divided by 64 using a while loop to determine the remaining The Base64 representation string starts with the remainder, which is then used to index the matching character from the Base64 character set.
The Base10 integer is updated via integer division (//) to continue the procedure after each division. Characters are added starting with the least significant digit and working up to the most significant digit to create the final Base64 representation. The divide-and-remainder method is exemplified and the outcome displays the manual Base10 to Base64 conversion
Handling Edge Cases
Base10 to Base64 conversion is simple, but handling edge circumstances is crucial for accuracy and dependability. If you preserve all digits while working with huge numbers, make sure you divide continuously until the quotient equals 0. Negative numbers require extra care; before starting the Base64 conversion, convert them to Two’s Complement binary representation. When working with floating-point numbers, one must first separate them into their integer and fractional parts before merging the resulting numbers using a separator.
Keep an eye out for any potential overflow in your Base64 representation and take into account any necessary splitting or truncation. While non-standard characters demand careful encoding attention, padding with ‘=’ characters ensures representation length integrity.
Practical Applications
The Base10 to Base64 conversion is important practically across domains. By allowing for the efficient transmission of graphics and multimedia via a number of channels, Base64-encoded data streamlines data transfer. It makes direct picture embedding within HTML possible for web development.
Secure information exchange is made possible by encoding cryptographic keys and signatures. A strong data flexibility canvas is produced by the Base10 to Base64 conversion, which enhances modern data manipulation, security, and communication.
Conclusion
Base10 to Base64 conversion emerges as a pivotal link in the complex dance between numbers and technology. Security is promoted, data transfer performance is improved, and multimedia integration is simplified with this. This journey goes beyond numbers to produce a digital mosaic where human understanding and machine efficiency reside together and illustrate the elegance of encoding.



