Optimizing Job Assignments with Python: A Greedy Approach

In this article, we will learn the skill of job assignment which is a very important topic in the field of Operations Research. For this, we will utilize Python programming language and the Numpy library for the same. We will also solve a small case on a job assignment.

Job assignment involves allocating tasks to workers while minimizing overall completion time or cost. Python’s greedy algorithm, combined with NumPy, can solve such problems by iteratively assigning jobs based on worker skills and constraints, enabling efficient resource management in various industries.

What is a Job Assignment?

Let us understand what a job assignment is with an example. In our example, three tasks have to be completed. Three workers have different sets of skills and take different amounts of time to complete the above-mentioned tasks. Now our goal is to assign the jobs to the workers to minimize the period of completing the three tasks.

Now, we solve the above problem using the concepts of Linear programming. Now there are certain constraints as well, each worker can be assigned only a single job at a time. Our objective function is the sum of all the time taken by the workers and minimize it. Let us now solve this problem using the power of the Numpy library of Python programming language.

import numpy as np
from scipy.optimize import linear_sum_assignment

# Define the completion times matrix
completion_times = np.array([
    [3, 5, 2],  # Task1
    [2, 1, 4],  # Task2
    [4, 3, 6]   # Task3
])

# Solve the assignment problem
row_indices, col_indices = linear_sum_assignment(completion_times)

# Print the results
tasks = ['Task1', 'Task2', 'Task3']
workers = ['Worker1', 'Worker2', 'Worker3']
for i, task in enumerate(tasks):
    worker = workers[col_indices[i]]
    completion_time = completion_times[i, col_indices[i]]
    print(f"{task} is assigned to {worker} with completion time {completion_time}")

Let us now look at the output of the problem.

Job Assignment Output — ***Optimal Job Assignment: A Simple Example***

From the output, we can see that The assignment is complete and optimized. Let us now look at a small case and understand the job assignment further.

A Real-World Job Assignment Scenario

Continuing with the example of assigning workers some jobs, in this case, a company is looking to get some work done with the help of some freelancers. There are 15 jobs and we have 10 freelancers. We have to assign jobs to workers in such a way, that we minimize the time as well as the cost of the whole operation. Let us now model this in the Python programming language.

import numpy as np

# Define data
num_jobs = 15
num_freelancers = 10

# Randomly generate job details: skill requirements, time constraints, pay rates
np.random.seed(0)
skills_required = np.random.randint(0, 2, size=(num_jobs, num_freelancers))  # Skills required for each job
deadlines = np.random.randint(1, 8, size=num_jobs)  # Deadlines for each job (days)
pay_rates = np.random.randint(10, 30, size=num_freelancers)  # Hourly pay rates for each freelancer ($/hr)

# Initialize assignment matrix
assignments = np.zeros((num_jobs, num_freelancers))

# Greedy assignment algorithm
for i in range(num_jobs):
    job_skills = skills_required[i]
    available_freelancers = np.where(np.sum(assignments, axis=0) < 3)[0]  # Find freelancers with fewer than 3 assignments
    available_freelancers_skills = job_skills[available_freelancers]
    freelancer_scores = np.dot(available_freelancers_skills, pay_rates[available_freelancers])
    best_freelancer = available_freelancers[np.argmax(freelancer_scores)]
    assignments[i, best_freelancer] = 1

# Print the results
for i in range(num_jobs):
    job_assigned = np.where(assignments[i] == 1)[0][0]
    print(f"Job {i+1} is assigned to Freelancer {job_assigned+1} with pay rate ${pay_rates[job_assigned]} per hour")

This problem is solved using the greedy algorithm. In short, the greedy algorithm selects the most optimal choice available and does not consider what will happen in the future while making this choice. In the above code, we have randomly generated data on freelancer details. Let us now look at the output of the code.

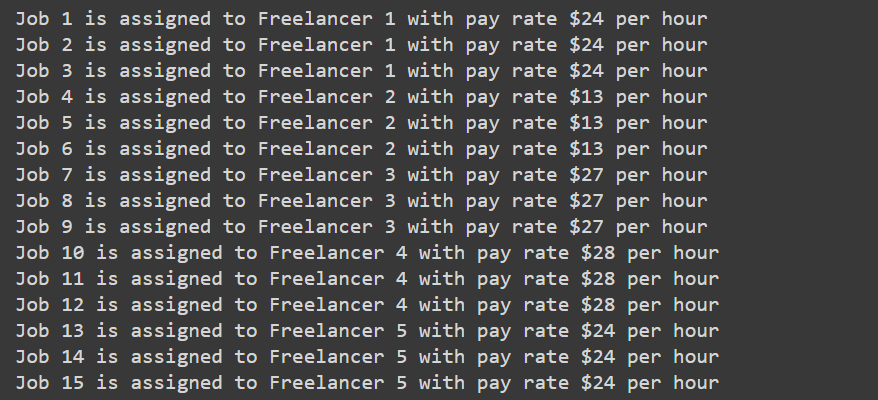
Job Assignment Case Study — ***Cost-Effective Job Assignments with Greedy Algorithm***

Thus, we complete our agenda of job assignment while minimizing costs as evidenced by the output.

Conclusion

Assigning jobs optimally is crucial for maximizing productivity and minimizing costs in today’s competitive landscape. Python’s powerful libraries like NumPy make it easy to implement greedy algorithms and solve complex job assignment problems, even with larger sets of jobs and workers. How could you adapt this approach to accommodate dynamic changes in job requirements or worker availability?