Numpy dot() – A Complete Guide to Vectors, Numpy, And Calculating Dot Products

In this article, we’ll learn about the numpy dot() method to find the dot products. It covers scalars. vectors, arrays, and matrices. It also involves real analysis and complex number applications, graph visualizations, and more. The real contribution of this subject is in the Data Science and Artificial Intelligence fields. 

What are Vectors?

A vector is a quantity in the form of an arrow with both direction and magnitude. That seems to be more precise to study. Now let’s dive a bit deeper into the concept of an arrow that we speak of here.

General definition and representation

1. Magnitude: A value or a specific number that a vector holds.
2. Direction: A flow from one point to another.

These are the details of those basic terms that in combination give birth to Vectors. We shall see the below image for the graphical representation of vectors along with a place.

How to Create a Matrix from a Vector

The most important operation of a vector is representing it in the form of a matrix or an array. Significantly i, j, and k are the directional components of a vector in the x, y, and z axes respectively. 

These three vectors can be transformed into a 3×3 matrix. The matrix presentation is:

[ [1, 2, -3], 
  [2, 3, 4], 
  [4, -1, 1] ]

In the same way, the implementation of the matrix from a given set of any vector is possible. Let us move towards the main topic which is taking a dot product. of two arrays.

Operations on Numpy Arrays

The list shows us the most important operations on vectors or arrays:

1. Dot product: addition of all products of the elements of two vectors. Represented as A.B.
2. Cross product: third vector which is resultant of two vectors. Represented as AxB.

In Python, there is a full library dedicated to Linear Algebra and its operations – Numpy. It stands for Numerical Python and it is for complex calculations especially under the involvement of n-dimensional arrays. It is an open-source library so, we can make it better by contributing to its code. It is an easily available API for the Python programming language. 

Implementing Numpy Arrays

The library is mainly in use for complex mathematical analysis and computations. So, to make it more probable make sure we study some of its basics. The core data type of this module is NumPy ndarray. This predicts that the main operations are relative to array synthesis and calculations. Let us do a quick tutorial for it.

Example #1:

import numpy as np

list_1 = [23, 12, 3, 11]
print('Original list: ', list_1)

arr = nparray(list_1)
print('Numpy array: ', arr)

print('Data type of list_1', type(list_1))
print('Data type of arr', type(arr))

# Output
# Original list: [23, 12, 3, 11] 
# Numpy array: array([23, 12, 3, 11])
# <class: list>
# numpy.ndarray

Example #2:

import numpy as np

matrix = np.array([[2, 4, 5], [-1, -4, 8], [3, -1, 9]])
print('Our matrix is: ', matrix)

# output:
# Our matrix is: 
# array([[2, 4, 5], 
#        [-1, -4, 8],            
#        [3, -1, 9]])
#

Mathematical operations on Numpy arrays

This section talks about the implementation of mathematical operations. These operations seem to be very easy with single integers but, for arrays, it is quite a complex task.

1. Addition
2. Subtraction
3. Multiplication
4. Division of two arrays

Code:

import numpy as np
a = np.array([[2, 3, 4], [-1, 3, 2], [9, 4, 8]])
b = np.array([[4, -1, 2], [34, 9, 1], [2, 0, 9]])

addition = a + b
subtraction = a - b
multiplication = a * b
division = a / b

print('Addition of arrays  a and b is: ', addition)
print('Subtraction of arrays  a and b is: ', subtraction)
print('Multiplication of arrays  a and b is: ', multiplication)
print('Division of arrays  a and b is: ', division)

Output:

Numpy dot() product

This product is a scalar multiplication of each element of the given array. In general mathematical terms, a dot product between two vectors is the product between their respective scalar components and the cosine of the angle between them. So, if we say a and b are the two vectors at a specific angle Θ, then 

a.b = |a|.|b|.cosΘ # general equation of the dot product for two vectors

But, in the dot() function of the Numpy array, there is no place for the angle Θ. So, we just need to give two matrices or arrays as parameters. Thus, we shall implement this in a code:

import numpy as np

var_1, var_2 = 34, 45 # for scalar values
dot_product_1 = np.dot(var_1, var_2)
dot_product_1

# for matrices
a = np.array([[2, 3, 4], [-1, 3, 2], [9, 4, 8]])
b = np.array([[4, -1, 2], [34, 9, 1], [2, 0, 9]])


dot_product_2 = np.dot(a, b)
dot_product_2

Output:

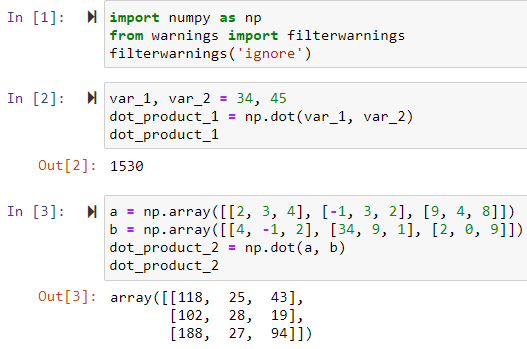
Code explanation:

1. Import the module Numpy.
2. After that declare two variables var_1 and var_2.
3. Call the np.dot() function and input all those variables inside it. Store all inside a dot_product_1 variable.
4. Then print it one the screen.
5. For multidimensional arrays create arrays using the array() method of numpy. Then following the same above procedure call the dot() product. Then print it on the screen.

A functional approach to Numpy dot() product

When we define functions in any programming language the code is very useful as we can call them randomly and essentially anytime. Thus, we will declare a function to make a good reach for calculating the dot product.

Code:

import numpy as np

def dot_product(array_1, array_2):
    prod = np.dot(array_1, array_2)
    return prod


def main():
    # declaring two empty arrays
    arr_1 = []
    arr_2 = [] 


    # taking user input for array 1
    n = int(input('Enter the number of elements for array_1: '))
    for i in range(n):
        arr_1.append(int(input('Enter number : ').strip()))
    
    # taking user input for array 2
    m = int(input('Enter the number of elements for array_2: '))
    for i in range(m):
        arr_2.append(int(input('Enter number: ').strip()))
        
        
    print('First array', arr_1, '\n'); print('Second array', arr_2, '\n')
    
    print('The dot product of arrays is: ', dot_product(arr_1, arr_2))
    
main()        

Explanation:

1. First we import the numpy module as np.
2. Then we declare a simple function – dot_product() that takes two arrays as parameters. The body of the function has the general np.dot() method called inside it that calculates the dot profuct and stores it inside the prod variable. Then the function returns the same at the end.
3. After that in the main function we declare two empty lists that are our arrays.
4. The variable ‘n’ takes input for the number of elements in the array_1.
5. Same is for variable ‘m’.
6. Then we run two for loops to take the elements for the arrays.
7. The for loop iterates within the range of the two variables n and m. Accordingly we input the values using the append function.
8. Same is for the second for loop.
9. After that we show the two arrays on the screen.
10. Then call our dot_product() function for taking the dot product and give those two arrays as parameters inside it.
11. After display the value on the screen.

Output:

Conclusion

So, in this way the topic ends. We saw the mathematical implementation of vectors and how they are closely related to arrays. Then we saw some transformations and complex mathematical calculations through code and image basis. After that basics of the Numpy module along with the dot() method for the dot product.