Normalization of the matrix is to scale the elements of the matrix in such a way that their values remain between zero and one. Depending on the order of a matrix, the function linalg.norm() returns one of the seven/eight different matrix norms or in some cases one of the many infinite matrix norms depending on the value of the order of the matrix.
Normalization helps in scaling huge data values into a reasonable numerical range so that the smaller values are not overpowered by larger values in model training algorithms. It helps in making the machine learning algorithms less sensitive to the scale of characteristics. Normalization rescales the element of a matrix into a specific magnitude without changing its direction.
Also read: Numpy linalg.eigvals – Compute the eigenvalues of a general matrix
Installing Numpy
In order to use this function you would need to have numpy installed in your system if you don’t already have it. Run the following code in your command prompt to install numpy. Make sure you run the command prompt in administrator mode for proper installation of the package.
pip install numpy.
In case you’re using anaconda or spyder for python projects then you have to run the code given below in your command prompt while in administrator mode:
conda install -c anaconda numpy
Also read: Numpy linalg.inv – Compute the (multiplicative) inverse of a matrix
Syntax of the Numpy linalg.norm() function
numpy.linalg.norm(m, ord, axis)
The parameters are:
m: arraylike: This is the input matrix whose normalization is to be computed.ord: int or none type (optional): The order of the normalization.axis:none type: returns a vector or a matrix norm and if it is an integer value, it specifies the axis along with the vector norm of the matrix m will be computed.
The function returns R : which is the normalized matrix or vector(s).
Some examples of the Numpy linalg.norm() function
Let’s look at a few examples of the numpy linalg.norm() function.
Example 1: Simple illustration of a predefined matrix
The first example is a simple illustration of a predefined matrix whose norm can be calculated as shown below:
#from numpy calling the function
import numpy as py
#pre defined matrix
m=[[4,2],[1,3]]
print("the initial matrix is=")
print(m) #displaying the matrix
print("The normalized result is=:")
#using the function
R=py.linalg.norm(m)
#displaying the result
print(R)
The output of the above code would be:
the initial matrix is=
[[4, 2], [1, 3]]
The normalized result is=:
5.477225575051661

2nd Example: Take a random matrix and normalize it
In this example, we will take a random matrix and normalize it using the numpy.linalg.norm() function.
#from numpy calling the function
import numpy as py
num=py.random.random() #generating random number using the function random
#creating the random matrix
m = py.array([[py.sin(num), -py.cos(num)], [py.cos(num), py.sin(num)]])
print("the initial matrix is=")
print(m) #displaying the matrix
#using the function
print("The normalized matrix is:")
R=py.linalg.norm(m)
#displaying the result
print(R)
The output of the above code will be:
the initial matrix is=
[[ 0.27126711 -0.96250411]
[ 0.96250411 0.27126711]]
The normalized matrix is:
1.4142135623730951

3rd Example: Normalize a matrix across a particular axis
Now, let us normalize a matrix across a particular axis by specifying the axis parameter.
#from numpy calling the function
import numpy as py
#predefined matrix
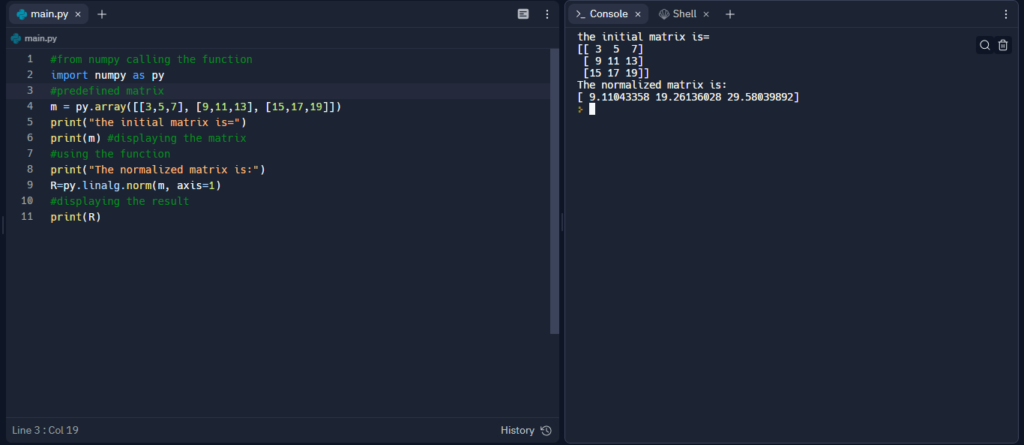
m = py.array([[3,5,7], [9,11,13], [15,17,19]])
print("the initial matrix is=")
print(m) #displaying the matrix
#using the function
print("The normalized matrix is:")
R=py.linalg.norm(m, axis=1)
#displaying the result
print(R)
The output of the above code would be:
the initial matrix is=
[[ 3 5 7]
[ 9 11 13]
[15 17 19]]
The normalized matrix is:
[ 9.11043358 19.26136028 29.58039892]
4th Example: Take user inputs for the values of the matrix and axis
Last but not the least, let’s take user inputs for the values of the matrix and then prompt the user to define an axis for normalization.
#from numpy calling the function
import numpy as py
#taking user input
row = int(input("Enter the number of rows:"))
col= int(input("Enter the number of columns:"))
num=int(input("specify one axis accross which the matrix is to be normalized"))
# Initializing the required matrix
m = []
print("enter the values rowwise:")
# For user input
for i in range(row): # loop for row entries
b =[]
for j in range(col): # loop for column entries
b.append(int(input()))
m.append(b)
print("the initial matrix is=", m)
#normalizing
result= py.linalg.norm(m, axis=num)
#displaying the result
print("the normalized matrix is=",result)
the output of the above code would be:
Enter the number of rows:3
Enter the number of columns:3
specify one axis accross which the matrix is to be normalized1
enter the values rowwise:
4
7
10
13
16
19
22
25
28
the initial matrix is= [[4, 7, 10], [13, 16, 19], [22, 25, 28]]
the normalized matrix is= [12.84523258 28.03569154 43.50861984]

Summary
The package numpy has a lot of extremely useful and efficient functions that can be used for scientific calculations which can be tedious and lengthy otherwise. To know more about numpy and its various functions and features visit the official site.



