In this tutorial, we will be understanding a very interesting problem known as The Tiling Problem. Let us first understand what do we want to achieve in this problem.
Understanding the Tiling Problem
In the Tiling Problem, we would be given a wall of size 4*n which means the height of the wall is 4 and the length of the wall is n ( will be taken from the user).
Now we would be having an infinite number of small tiles of size 4*1 which can be arranged on the wall in two different ways. The same is displayed in the image below.
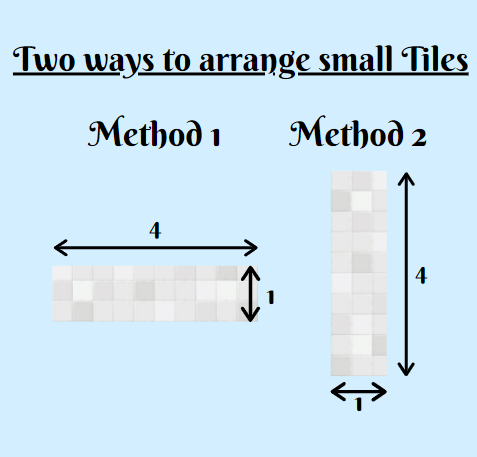
Our aim is to count all the possible patterns using the small tiles in either of the methods mentioned above in order to fill the whole wall.
Solution to the Tiling Problem in Python
One can either manually code the naive approach using loops and if-else conditions or can go for the faster approach which is the Recursion approach. If you want to know more about recursion read the tutorial mentioned below.
Read more about Recursion: Recursion in Python
Using recursion, we will be dividing a big problem into smaller problems. Now here let’s take a look at the smaller problems in both arrangements.
- Arrangement 1: First tile is put according to Method 1 which decreases the length of the wall by 4 and the space left above the current tile can only be filled in one way ( 3 tiles according to Method 1 )
- Arrangement 2: Secondly we can put the first tile according to Method 2 which decreases the length of the wall by 1.
After the first arrangement is done. We recursively call the same operations for the remaining wall by calling the same function but with a decreased value of n.
The final solution would be the sum of the possible ways in both the arrangements in each recursive call. Let’s understand for a few examples through a small illustration displayed below.

Implementing the Solution to the Tiling Problem in Python
def find_count_arrangements(n):
if(n<=3):
return 1
return find_count_arrangements(n-1) + find_count_arrangements(n-4)
n = int(input())
print(find_count_arrangements(n))
The code implementation is very simple through recursion. Just make sure you have understood the solution explained earlier.
I hope you understood the problem statement, solution, and code implementation of the tiling problem. Thank you for reading!
Happy Learning! 😇



