Tower of Hanoi in Python: Complete Step-by-Step

By /
TOWER OF HANOI IN PYTHON

Tower of Hanoi is a mathematical problem (puzzle) that consists of 3 poles and ‘n’ number of discs, each disc having different diameters.

The Objective of the Tower of Hanoi Problem

The objective or goal of this problem is to transfer all the ‘n’ discs from source pole to the destination pole in such a way that we get the same arrangement of discs as before. But this goal must be achieved by sticking to the rules.

Rules and Constraints

The constraints that must be satisfied while solving the problem are –

  1. Only one disc can be moved at a time.
  2. Only the top-most disc can be removed
  3. The larger disc cannot be placed on top of the smaller disc.

Visual Representation of the Tower of Hanoi problem

The following picture shows the step-wise solution for a tower of Hanoi with 3 poles (source, intermediate, destination) and 3 discs. The goal is to move all the 3 discs from pole A to pole C.

STEP 1
STEP 3 4
STEP 5 6
STEP 7 8

As we can see from the above solution, the number of moves needed for 3 discs = 8. So, a generalized formula for a total number of moves we need is:

Total number of moves = n2 – 1

Where ‘n’ is the total no. of discs.

Solving the Tower of Hanoi Problem in Python

def TowerOfHanoi(n , s_pole, d_pole, i_pole):           
    if n == 1:
        print("Move disc 1 from pole",s_pole,"to pole",d_pole)
        return
    TowerOfHanoi(n-1, s_pole, i_pole, d_pole)
    print("Move disc",n,"from pole",s_pole,"to pole",d_pole)
    TowerOfHanoi(n-1, i_pole, d_pole, s_pole)

n = 3
TowerOfHanoi(n, 'A', 'C', 'B')
# A, C, B are the name of poles

In the above code, we call our function TowerOfHanoi recursively for 3 discs.

Here:

  • s_pole: source pole
  • i_pole: intermediate pole
  • d_pole: destination pole

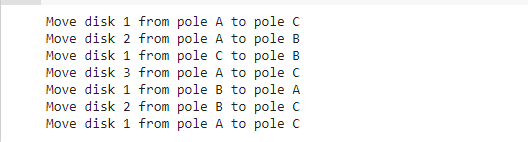
The output of the above code is:

Output 1

Conclusion

So , this is how we solve the problem of Tower of Hanoi.

This code can be generalized for any number of discs. So if you want the solution for 4 discs, just change the value of n from 3 to 4 as n = 4, and the output will be displayed for 4 discs and so on.