Jaccard Similarity and Jaccard Index using Python and NLP

Jaccard Distance and Jaccard Similarity (also called as Jaccard Index) are a measurement of similarity between two sets in Set Theory. Jaccard Similarity is highly useful in Natural Language Processing, as they can give a similarity measure between two words or sentences to a certain level. Jaccard Similarity is a measure of similarity between two sets, which means higher the value of Jaccard Similarity, the more similar the two sets are. Jaccard Distance on the other hand, is counterpart of Jaccard Similarity, and it is a measurement of how dissimilar two sets are. It calculates the distance between two sets. Hence lower the value, more closer or more similar two sets are to each other.

The concept of Jaccard Similarity and Jaccard Distance is completely based on Set Theory and uses basic Set Operations to calculate the same. It is calculated as follows:

In the above formula, the Numerator is the number of elements common in sets A and B, the Intersection of Set A and B. The denominator is the total number of elements in sets A and B, the Union of set A and B. It should be noted that sets are being used over here, and so the rules of sets need to be followed as well. Duplicate elements are removed from the set in Intersection and Union before taking their ordinals. The Jaccard Distance is calculated as follows:

In the above formula, the operator in Numerator is the Symmetric Difference. It can be learned from this article, that number of elements in Symmetric Difference is basically the difference between number of elements in Union and number of elements in Intersection. Putting this as the value of Symmetric Difference in the above formula yields the following result:

It can be simply written as:

So basically, Jaccard Distance is Jaccard Similarity of two sets, subtracted from 1. But this basic formula is not enough to calculate similarity between two words/sentences in Natural Language Processing. To understand the reason, Jaccard Distance needs to be implemented in Python, and then the results on a few words will describe the inefficient output. A more stricter version of Jaccard Similarity and Jaccard Distance will be used to calculate similarity between two words/sentences in Natural Language Processing.

Implementation of Jaccard Similarity and Jaccard Distance

The Python data structure sets will be used here for implementation. Sets are lists, but they do not have duplicate elements. A list can be converted to set using the set() function. The implementation of Jaccard Similarity is shown below:

def JaccardSimilarity(firstset,secondset):
  list1=list(firstset)
  list2=list(secondset)
  union=0
  intersection=0
  set1=set(list1)
  set2=set(list2)
  for element in set1:
    if element in set2:
      intersection=intersection+1
  unionlist=list1+list2
  unionset=set(unionlist)
  union=len(unionset)
  js=intersection/union
  return js

As it can be seen in the above code snippet, the inputs to function JaccardSimilarity(), namely firstset and secondset, are firstly converted to lists and lists are worked upon. This is done to convert any kind of other data structure, such as strings or tuples, into list before proceeding. The union and intersection variables hold the number of items in union and intersection sets. It should be noted that the union() and intersection() functions of Set data structure can also be used to get the aim, but here they have been implemented individually for better explanation. Both the lists are converted to sets, and the duplicate elements from those lists are eliminated. Now each element in the first set is iterated through, and if found in the second set, the intersection variable is incremented by 1. Another set is created called the unionset, which is the set of both the lists combined. Its length is assigned as the union variable. The jaccard similarity is intersection variable divided by union variable.

As explained above, Jaccard Distance is nothing but Jaccard Similarity, subtracted from 1. Hence the following will be Jaccard Distance’s Implementation:

def JaccardDistance(word1,word2):
  return 1-JaccardSimilarity(word1,word2)

The above function uses the already implemented JaccardSimialrity() function. Now, the following two lists will be provided as input to JaccardSimilarity() and JaccardDistance() functions to check their outputs:

set1=[1,1,4,5,7,9,0,6,5]
set2=[9,6,3,6,4,0,1,2,1]
print('Jaccard Similarity: '+str( JaccardSimilarity(set1,set2)))
print('Jaccard Distance: '+ str(JaccardDistance(set1,set2)))

It produces the following output:

The output is as expected. The lists after conversion to sets become {1,4,7,5,9,0,6} and {1,2,3,4,0,6,9}. The union has 9 elements {1,4,7,5,9,0,6,2,3}, and their intersection has 5 elements {1,4,6,9,0} . So the output of JaccardSimilarity() is 5/9=0.555556, and the output of JaccardDistance() is 4/9=0.4444444444.

But the problem now occurs when JaccardSimilarity() function is used to calculate similarity between two words/sentences. To present the fact, a few words have been used as an example. On running the following code:

listofwords=['list','set','tuple','jaccard','jackal','distance','index','article','python','mobile','computer','square']
for word in listofwords:
  print(word)
  print(JaccardSimilarity(word,word))

The following output is produced:

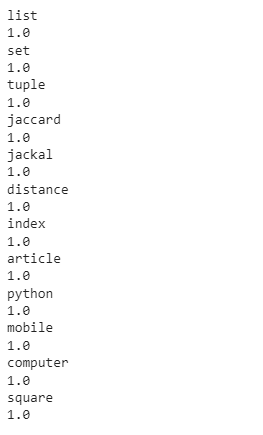
This is expected output, as same words shall produce a 1.0 JaccardSimilairty(). But what will happen if some of these words are purposefully misspelled. The following code does the same:

listofwords=['list','set','tuple','jaccard','jackal','distance','index','article','python','mobile','computer','square']
fakewords=['lits','set','tulp','jakard','jakal','ditsance','idnex','articel','typhoon','mobeel','computer','sqaure']
for i in range(len(listofwords)):
  print(listofwords[i]+' '+fakewords[i])
  print(JaccardSimilarity(listofwords[i],fakewords[i]))

It should be noted that some of these words, such as ‘square’ and ‘sqaure,’ have minor differences, but ‘sqaure’ is a wrong spelling, and for that reason, the JaccardSimilarity() should not return 1.0 . But this is the output observed from the code:

It works perfectly on some words such as ‘jaccard’ and ‘jakard,’ but for most of the misspelled words such as ‘index’ and ‘idnex’ or ‘article’ and ‘articel,’ JaccardSimilarity() returns the value 1.0; which is not acceptable. Hence, a stricter version of JaccardSimilarity() needs to be implemented for Natural Language Processing.

Jaccard Similarity and Jaccard Distance for NLP

The base idea behind Jaccard Similarity for NLP is that the strings of words are not converted to sets, and the letters of these words are included in the Intersection set if and only if the letter is present at the same position in both the lists. Using these stricter conditions, JaccardSimilarity() provides a more accurate result in matching word similarity than the original idea. It is shown in the following code:

def JaccardSimilarityforNLP(word1,word2):
  list1=list(word1)
  list2=list(word2)
  iter=min(len(list1),len(list2))
  union=len(set(list1+list2))
  intersection=0
  for i in range(iter):
    if list1[i]==list2[i]:
      intersection=intersection+1
  ji=intersection/union
  return ji

In the above code snippet, the code runs a for loop for a number of iterations, where the number is the length of the smaller word. A letter is considered in the intersection set, if it is present in both lists at the same position. The union is calculated as same method used earlier. Using this algorithm, Jaccard Similarity provides a clearer similarity between two words. It can be seen on running the following code:

listofwords=['list','set','tuple','jaccard','jackal','distance','index','article','python','mobile','computer','square']
fakewords=['lits','set','tulpe','jakkard','jakcal','ditsance','idnex','articel','typhon','mobeel','computer','sqaure']
for i in range(len(listofwords)):
  print(listofwords[i]+' '+fakewords[i])
  print(JaccardSimilarityforNLP(listofwords[i],fakewords[i]))

It provides the following output:

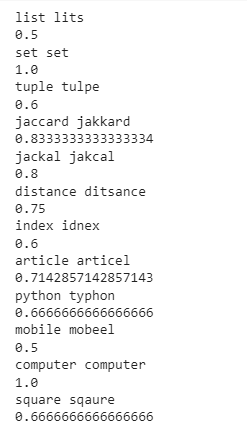
This provides a more clear based idea on similarity between two different words. But it should be noted that Jaccard Distance works better with words/sentences having the same length. Edit Distance is a better metric to measure similarity between two words with different lengths.

It should also be noted that the Jaccard Similarity does not always provide an exact 1.0 for the same words. Sometimes, the value can be greater than 1. It happens because the number of elements in the intersection defined, can be more than the elements in union of the two words. Two different words will definitely have a Jaccard Similarity (in this case) smaller than 1, but two same words can have Jaccard Similarity either equal to or greater than 1. It can be seen in the following example:

listofwords=['list','set','tuple','jaccard','jackal','distance','index','article','python','mobile','computer','square']
for word in listofwords:
  print(word)
  print(JaccardSimilarityforNLP(word,word))

It produces the following output:

Two same words will never have a Jaccard Similarity (in this case) smaller than 1.

Metrics such as Jaccard Distance and Jaccard Similarity are also implemented more accurately in different Python Natural Language Processing libraries such as NLTK and SpaCy. Their implementations also cover up the inaccuracies left out in this implementation. The links to their official documentations are NLTK and SpaCy

Conclusion

Word based similarity matching is highly important in Natural Language Processing. Jaccard Distance and Jaccard Similarity are useful for measuring the similarity between two sets. As the words and sentences in NLP can be treated as sets, Jaccard Distance and Jaccard Similarity also provide a metric for measuring word/sentence similarity. Their rules must be stricter for a successful implementation, as normal Jaccard Similarity will fail to measure similarities in NLP. Checking that a letter exists at the same position in two equally long words/sentences and considering only those elements in Intersection set provides a better output than normal Jaccard Similarity.

Similarity matching can lead to several useful NLP-based applications, such as Chatbots and Translators. This article teaches on how to make a Chatbot in Python using SpaCy’s Similarity Matching.

Frequently Asked Questions about Jaccard Similarity and Jaccard Distance